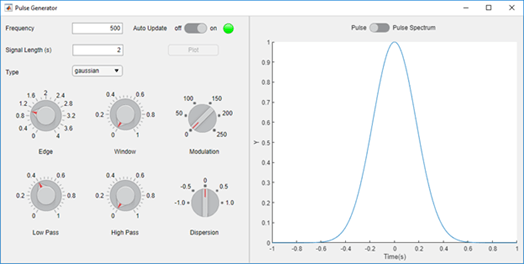
https://kr.mathworks.com/help/matlab/creating_guis/app-or-gui-with-instrument-controls.html
그리드 레이아웃을 사용하여 구성요소 위치와 크기 조정을 관리하는 앱 - MATLAB & Simulink - MathWorks
이 예제의 수정된 버전이 있습니다. 사용자가 편집한 내용을 반영하여 이 예제를 여시겠습니까?
kr.mathworks.com
핵심코드
1) Properties (Access = Private)
프로그램 코드 작성 시 사용할 변수 선언
properties (Access = private) autoUpdate end |
2) methods (Access = Private)
2-1) Plot을 업데이트 하는 기능의 함수
function updatePlot(app) signalLength = app.SignalLengthsEditField.Value ; frequency = app.FrequencyEditField.Value ; plotType = app.PlotTypeSwitch.Value ; p = generatePulse(app) ; t = -signalLength/2:1/frequency:signalLength/2; if strcmp(plotType,'Pulse') plot(app.PulsePlotUIAxes, t, p); xlabel(app.PulsePlotUIAxes,'Time(s)'); else lp=length(p); Y=fft(p); sig=abs(Y(1:ceil(lp/2))); f=linspace(0, frequency/2, ceil(lp/2)); plot(app.PulsePlotUIAxes, f(sig>1e-4), sig(sig>1e-4)); xlabel(app.PulsePlotUIAxes,'Frequency (Hz)'); end end |
2-2) Pulse를 생성하는 기능의 함수
function result = generatePulse(app) frequency = app.FrequencyEditField.Value; signalLength = app.SignalLengthsEditField.Value; edge = app.EdgeKnob.Value; window = app.WindowKnob.Value; modulation = str2double(app.ModulationKnob.Value); lowpass = app.LowPassKnob.Value; highpass = app.HighPassKnob.Value; dispersion = str2double(app.DispersionKnob.Value); startFrequency = 10; stopFrequency = 20; t = -signalLength/2 : 1/frequency : signalLength/2; sig = (signalLength/(8*edge))^2; switch app.TypeDropDown.Value case 'gaussian' y = exp(-(t).^2/sig) ; case 'sinc' x = 2*pi*edge*50.*t/(5*signalLength) ; y = sin(x)./x ; y(x==0) = 1 ; case 'square' y = (t > -signalLength/edge/2) & (t < signalLength/edge/2) ; case 'triangle' y = (t + signalLength/edge/2).*(t < 0) - (t - signalLength/edge/2).*(t >= 0); y(y < 0) = 0 ; case 'monocycle' if (sig == 0) y = t ; else y = 2*t./sig.*exp(-(t).^2/sig) ; end case 'exponential' y = exp(-t*8*edge/signalLength) ; y(t<0) = 0 ; case 'biexponential' y = exp(-abs(t)*8*edge/signalLength) ; case 'mexican hat' z = t./sqrt(0.75*sig); y = sqrt(1/2*pi).*(1-z.^2).*exp(-z.^2/2) ; case 'raised cosine' rb = 2*edge*50/(5*signalLength); x = pi.*t.*rb ; y = sin(x)./x ; y(x==0) = 1 ; y = y.*(cos(2*pi*rb.*t)./(1 - (4*rb.*t).^2)); case 'double sinc' x1 = 2*stopFrequency*pi.*t ; x2 = 2*startFrequency*pi.*t ; y1 = sin(x1)./x1 ; y1(x1==0) = 1 ; y2 = sin(x2)./x2 ; y2(x2==0) = 1 ; y = stopFrequency*y1 - startFrequency*y2; case 'sinc squared' x = 2*pi*edge*16.*t/(5*signalLength) ; y = sin(x)./x ; y(x==0) = 1 ; y = y.^2 ; case 'sweep' theta = startFrequency.*(t + signalLength/2) + ... ((stopFrequency - startFrequency)/(signalLength)).*(t+signalLength/2).^2; y = real(exp(1j*(2*pi.*theta - pi/2))); end if (lowpass < 1) || (highpass > 0) || (dispersion ~= 0) c = length(y) ; end s = fft(y); sA = abs(s); sP = angle(s); if (lowpass < 1) cP = ceil(lowpass*c/2); if (cP == 0) sA(:) = 0; else sA(cP:end-cP+2) = 0; end end if (highpass > 0) cP = floor(highpass*c/2); if (cP ~= 0) sA(1:cP) = 0; sA(end-cP+2:end) = 0; end end if (dispersion ~= 0) pp = dispersion.*linspace(0,2*pi,c); sP = sP + pp; end s2 = sA.*cos(sP) + 1j*sA.*sin(sP); y = real(ifft(s2)); if (window > 0) c = length(y); w = ones(size(y)); p1 = floor(c*window/2); % Window is defined in three sections: taper, constant, taper w(1:p1+1) = (-cos((0:p1)/p1*pi)+1)/2; w(end-p1:end) = (cos((0:p1)/p1*pi)+1)/2; y=w.*y; end if modulation ~= 0 y = y.*cos(pi*t*modulation); end result = y./max(abs(y)) ; end end |
3) Callback Function
3-1) 앱이 시작될 때 데이터 로딩 및 초기화를 수행하는 기능
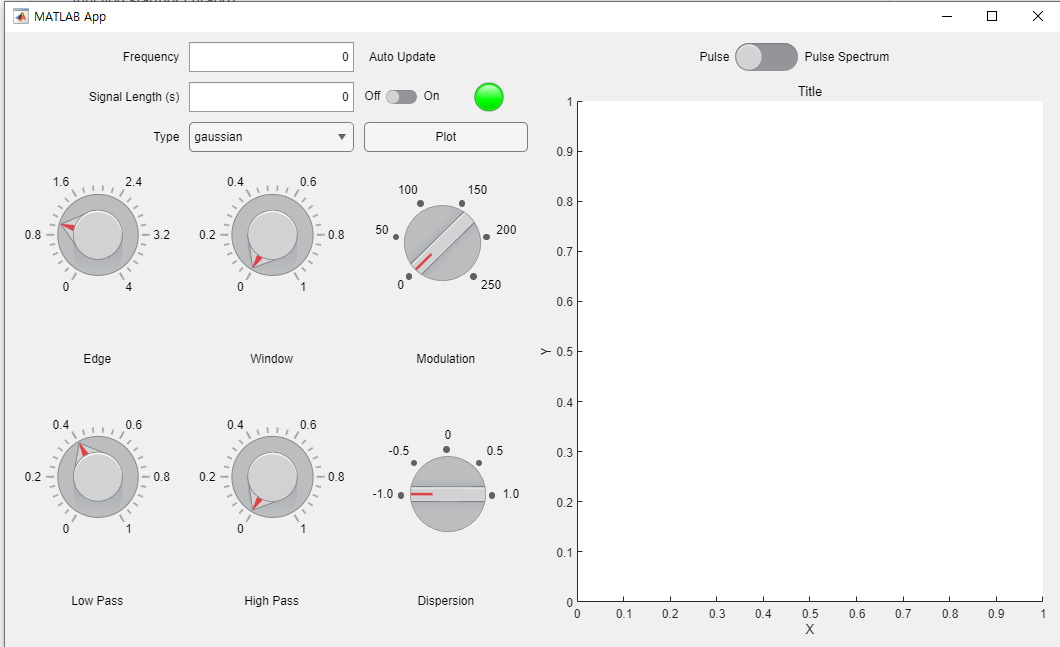
function startupFcn(app) app.AutoUpdateSwitch.Value = 'on'; app.PlotTypeSwitch.Value = 'Pulse'; app.PlotButton.Enable = 'off'; app.autoUpdate = 1; updatePlot(app) end |
3-2) Plot 버튼을 Push할 때의 콜백함수
function PlotButtonPushed(app, event) updatePlot(app) end |
3-3) Auto Update의 스위치를 변환할 때의 콜백함수
function AutoUpdateSwitchValueChanged(app, event) if strcmp(app.AutoUpdateSwitch.Value, 'on') app.autoUpdate = 1; app.PlotButton.Enable = "off"; app.AutoUpdateLamp.Color = [0 1 0]; else app.autoUpdate = 0; app.PlotButton.Enable = 'on'; app.AutoUpdateLamp.Color = [0.5 0.5 0.5]; end end |
3-4) Edge Knob의 값이 변화할 때의 콜백함수
function EdgeKnobValueChanged(app, event) if app.autoUpdate updatePlot(app) end end |



