
12. 고급 정렬 알고리즘
고급 정렬 알고리즘은 효율적으로 데이터를 정렬하기 위해 개발된 알고리즘.
이러한 알고리즘들은 일반적으로 일반적인 정렬 알고리즘인 버블 정렬이나
삽입 정렬보다 더 효율적인 성능을 제공함.
| 분할 정복(Divide and Conquer): 큰 문제를 작은 하위 문제로 분할하고, 각 하위 문제를 재귀적으로 해결한 다음, 그 결과를 결합하여 원래 문제의 해답을 얻는 알고리즘 설계 기법. 주요 아이디어: 1) 분할(Divide): 원래 문제를 작은 부분 문제로 분할. 문제를 반으로 쪼개는 것이 일반적이지만, 경우에 따라 다른 방식으로 분할할 수도 있음. 2) 정복(Conquer): 각 하위 문제를 재귀적으로 해결. 하위 문제가 충분히 작아서 직접 해결할 수 있는 경우에는 재귀 호출을 중단하고 해결함. 3) 결합(Combine): 각 하위 문제의 해답을 결합하여 원래 문제의 해답을 얻음. 문제를 더 작고 해결하기 쉬운 하위 문제로 분할함으로써 전체적인 문제 해결 과정을 간소화하는데 목적을 둠. 대부분의 분할 정복 알고리즘은 재귀적인 구조를 가지며, 이를 통해 문제의 크기를 점진적으로 줄여나감. 하향식 접근법(Top-down Approach)은 분할 정복과 관련있음. 이 접근법은 큰 문제를 해결하기 위해 재귀적으로 작은 하위 문제를 해결하는 방식으로, 문제를 작은 부분으로 나누고 각 부분을 해결하면서 최종적인 해답을 구성함. 이러한 접근법에서는 주로 재귀 함수를 사용하여 하위 문제를 해결하며, 이를 통해 분할 정복 알고리즘을 구현할 수 있음. 하향식 접근법에서는 문제를 작은 단위로 분할하고, 각 단계에서 필요한 계산을 수행하면서 전체적인 문제 해결 과정을 이끌어감. 이는 재귀 호출과 함께 사용되는 경우가 많음. |

시간 복잡도:
알고리즘을 수행하는 데 평균적으로, 또는 최악의 경우 얼마만큼의 시간이 걸리는 지를 확인.
복잡도는 주로 빅오 표기법을 사용해서 나타냄. 최악의 경우 걸리는 시간을 표기하는 방법인데,
아무리 최악이더라도 이 정도는 넘지 않겠구나라고 생각하면 됨.
아래 그래프에서 기울기가 가파를수록 성능이 좋지 않음.

12-1. 병합 정렬(Merge Sort)
병합 정렬은 분할 정복(Divide and Conquer) 알고리즘을 기반으로 하는 정렬 알고리즘.
큰 문제를 작은 문제로 분할한 다음, 작은 문제들을 해결하고 결과를 병합하여 정렬된 결과를 얻는 방식으로 작동.

주요 아이디어:
1) 분할(Divide):
정렬할 리스트를 절반으로 분할. 분할은 리스트의 크기가 1 이하가 될 때까지 재귀적으로 수행됨.
2) 정복(Conquer):
분할된 부분 리스트에 대해 재귀적으로 정렬을 수행합니다. 리스트의 크기가 충분히 작아지면 정렬을 중단하고, 그 부분 리스트를 반환합니다.
3) 병합(Combine):
정렬된 부분 리스트들을 병합하여 전체 리스트를 생성함.
이때, 각 부분 리스트에서 가장 작은 요소부터 차례대로 선택하여 병합함.
병합 정렬은 리스트를 반으로 분할하는 과정을 반복하면서 분할된 리스트를 정렬하고 병합하며,
이를 통해 최종적으로 정렬된 리스트를 얻을 수 있음. 시간 복잡도는 평균적으로 O(n log n)임.
병합 정렬은 안정적인 정렬 알고리즘으로 알려져 있으며, 대규모 데이터에 대해서도 효과적으로 동작함.
그러나 정렬하려는 리스트의 크기에 따라 추가적인 메모리 공간이 필요할 수 있으므로,
공간 복잡도에 대한 고려가 필요할 수 있음.
merge_sort(list[], p, r): if p < r: q <- |(p+r)/2| # 분할하기 위한 p, r의 중간지점 계산 merge_sort(list[], p, q) # 전반부 정렬 재귀 merge_sort(list[], q+1, r) # 후반부 정렬 재귀 merge(list[], p, q, r) # 병합 merge(list[], p, q, r): 정렬된 두 리스트 list[p...q], list[q+1...r]을 합쳐 정렬된 하나의 리스트 list[p...r]을 만듦 merge(list[], p, q, r): # prev, curr, next 역할 : 포인터 i <- p j <- q+1 t <- 0 # 옮겨담을 새로운 리스트 tmp에 대한 인덱스 while i <= q and j <= r if list[i] <= list[j] tmp[t] <- list[i] t++; i++ else tmp[t] <- list[j] t++; j++ while i <= q # 왼쪽 부분 리스트가 남은 경우 tmp[t] <- list[i] t++; i++ while j <= r # 오른쪽 부분 리스트가 남은 경우 tmp[t] <= list[j] t++; j++ i <- p; t <- 0 # 다 옮겼으면 원래꺼에 복사할 준비 while i <= r list[i] <- tmp[t] i++; t++ |
12-1-1. 구현
def merge_sort(alist, p: int, r: int):
if p < r:
q = (p+r) // 2
merge_sort(alist, p, q)
merge_sort(alist, q+1, r)
merge(alist, p, q, r)
def merge(alist, p: int, q: int, r: int):
i = p; j = q+1; t = 0
tmp = [0 for _ in range(len(alist))]
while i <= q and j <= r:
if alist[i] <= alist[j]:
tmp[t] = alist[i]
t += 1; i += 1
else:
tmp[t] = alist[j]
t += 1; j += 1
while i <= q:
tmp[t] = alist[i]
t += 1; i += 1
while j <= r:
tmp[t] = alist[j]
t += 1; j += 1
i = p; t = 0
while i <= r:
alist[i] = tmp[t]
t += 1; i += 1
12-1-2. 테스트
import random as r
ms_list = [r.randint(1,20) for _ in range(12)]
print(ms_list)
merge_sort(ms_list, 0, len(ms_list)-1)
print(ms_list)
12-2. 퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복(Divide and Conquer) 알고리즘을 기반으로 하는 정렬 알고리즘.
특히 평균적으로 빠른 속도와 효율성으로 알려져 있음.
주요 아이디어:
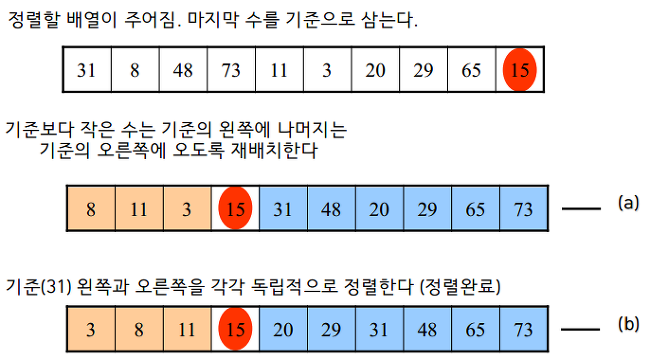
1) 분할(Divide):
정렬할 리스트에서 하나의 요소를 선택하고,
이를 기준으로 작은 요소는 왼쪽으로, 큰 요소는 오른쪽으로 분할함.
이렇게 하면 기준 요소가 자신의 최종 위치를 찾게 되며 이 과정을 파티셔닝(Partitioning)이라고 함.
2) 정복(Conquer):
분할된 부분 리스트에 대해 재귀적으로 정렬을 수행함.
파티셔닝된 왼쪽 부분 리스트와 오른쪽 부분 리스트에 대해 동일한 분할 과정을 적용함.
3) 결합(Combine):
정렬된 부분 리스트를 결합하여 최종적으로 정렬된 리스트를 얻음.
여기서는 이미 정렬된 부분 리스트들을 병합할 필요가 없음.
분할과정에서 기준 요소를 기준으로 작은 요소는 왼쪽에, 큰 요소는 오른쪽에 위치시키기 때문임.
시간 복잡도는 평균적으로 O(n log n)이지만, 최악의 경우에는 O(n^2)의 시간 복잡도를 가질 수 있음.
최악의 경우는 주로 이미 정렬된 리스트와 같이 기준 요소가 항상 최소값이나 최대값에 가까울 때 발생.
퀵 정렬은 불필요한 데이터 이동을 최소화하며, 재귀 호출을 사용하여 구현할 수 있음.
quick_sort(list[], p, r): if p < r q <- partition(list[], p, r) # 분할 기준점 찾기 quick_sort(list[], p, q-1) # 왼쪽 퀵정렬 재귀 quick_sort(list[], q+1, r) partition(list[], p, r): 리스트 list[p...r]의 원소들을 기준 원소인 list[k]와의 상대적 크기에 따라 양쪽으로 재배치하고, 기준 원소가 자리한 위치를 리턴 # pivot : 기준 원소 x <- list[r] # i가 작은 지역의 끝지점 (첫지점 p) : 1지역 i <- p - 1 # j가 아직 모르는 부분의 시작 지점 : 3지역 for j <- p to r-1 # 탐색 중 1구역 원소를 발견한다면 if list[j] < x # 1구역을 한 칸 늘리고, 탐색한 원소 list[j]랑 교환한다 list[++i] <-> list[j] # 기준점 제자리 찾기 : 3구역 원소와 교환 list[i+1] <-> list[r] # 정렬에서 제외할 기준점 리턴 return i+1 |
12-2-1. 구현
def quick_sort(alist, p: int, r: int) -> None:
if p < r:
q = partition(alist, p, r)
quick_sort(alist, p, q-1)
quick_sort(alist, q+1, r)
def partition(alist, p:int, r:int) -> int:
# pivot : 기준 원소
pivot = alist[r]
# i가 기준보다 작은 지역의 끝지점 : 1지역
i = p - 1
# j는 아직 모르는 부분(탐색 지점)의 시작 인덱스 : 3지역
for j in range(p,r):
# 탐색 중 1구역 원소(기준보다 작은 원소) 발견 시
if alist[j] < pivot:
# 1구역(기준보다 작은 지점)을 한 칸 먼저 늘린다
i += 1
# 탐색한 원소 list[j]랑 교환
alist[i], alist[j] = alist[j], alist[i]
# 배열리스트에서 기준점 제자리 찾기
alist[i+1], alist[r] = alist[r], alist[i+1]
# 다음 퀵정렬에서 제외할 기준점 리턴
return i+1
12-2-2. 테스트
import random as r
qs_list = [r.randint(1,20) for _ in range(8)]
print(qs_list)
quick_sort(qs_list, 0, len(qs_list)-1)
print(qs_list)
12-3. 힙 정렬(Heap Sort)
힙 정렬은 힙(Heap) 자료구조를 기반으로 한 정렬 알고리즘.
(힙은 완전 이진 트리의 일종으로, 특정한 조건을 만족하는 트리)
힙 정렬은 이러한 힙 자료구조를 이용하여 정렬을 수행.
주요 아이디어:
1) 힙 구성(Build Heap):
정렬할 리스트를 순회하며 조건을 만족하도록 힙 구조를 생성 및 구성함.
일반적으로는 Max 힙(부모 노드의 값이 자식 노드의 값보다 큰 경우)을 사용함.
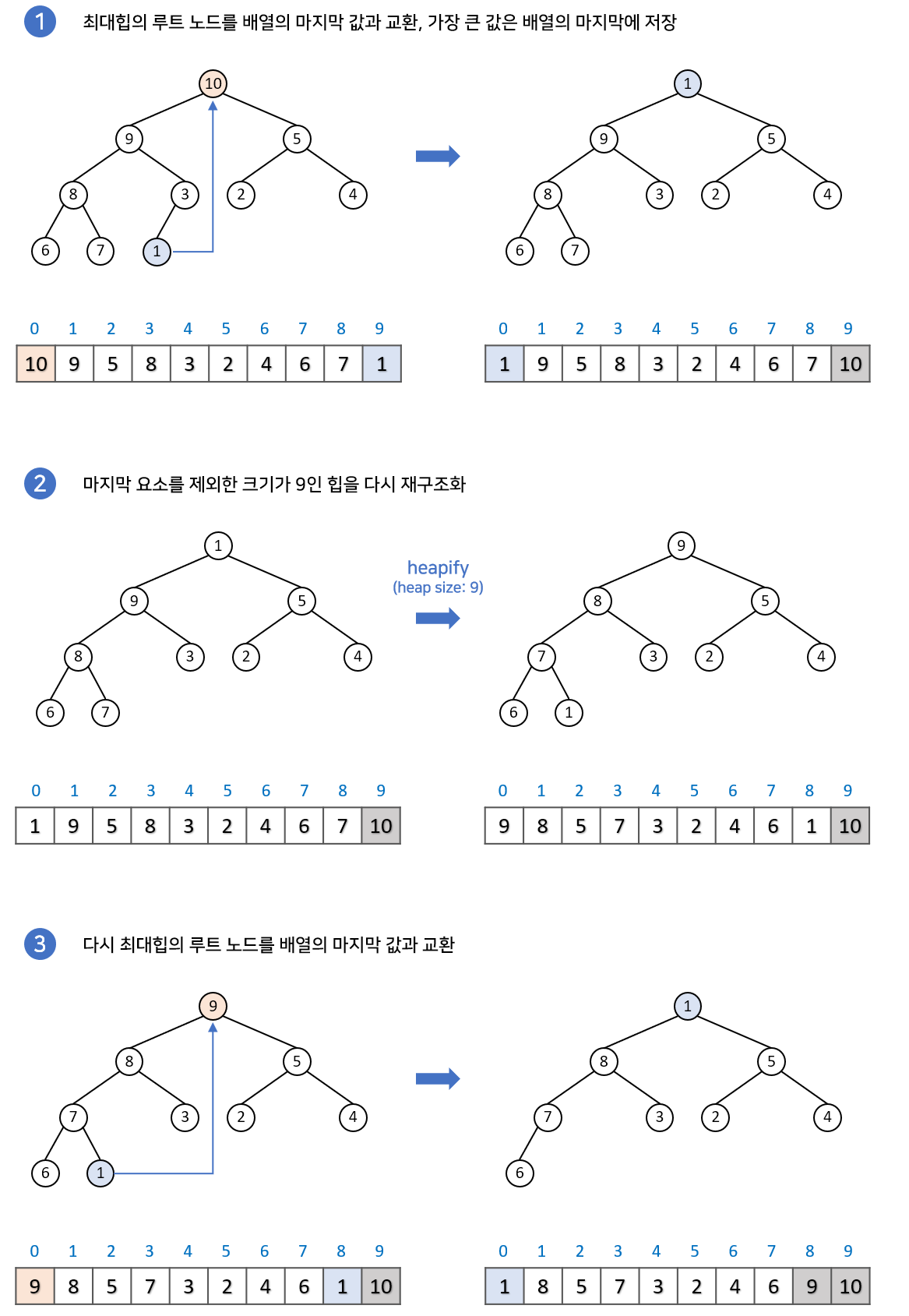
2) 최대값 추출(Extract Max):
힙에서 최대값(루트 노드)을 추출함. 추출한 값은 정렬된 리스트의 맨 뒤로 이동함.
3) 힙 재구성(Heapify):
힙에서 최대값을 추출한 후, 남은 요소들을 다시 힙 구조로 재구성함.
이 단계에서 힙 조건을 유지하기 위해 필요한 조정 작업을 수행함.
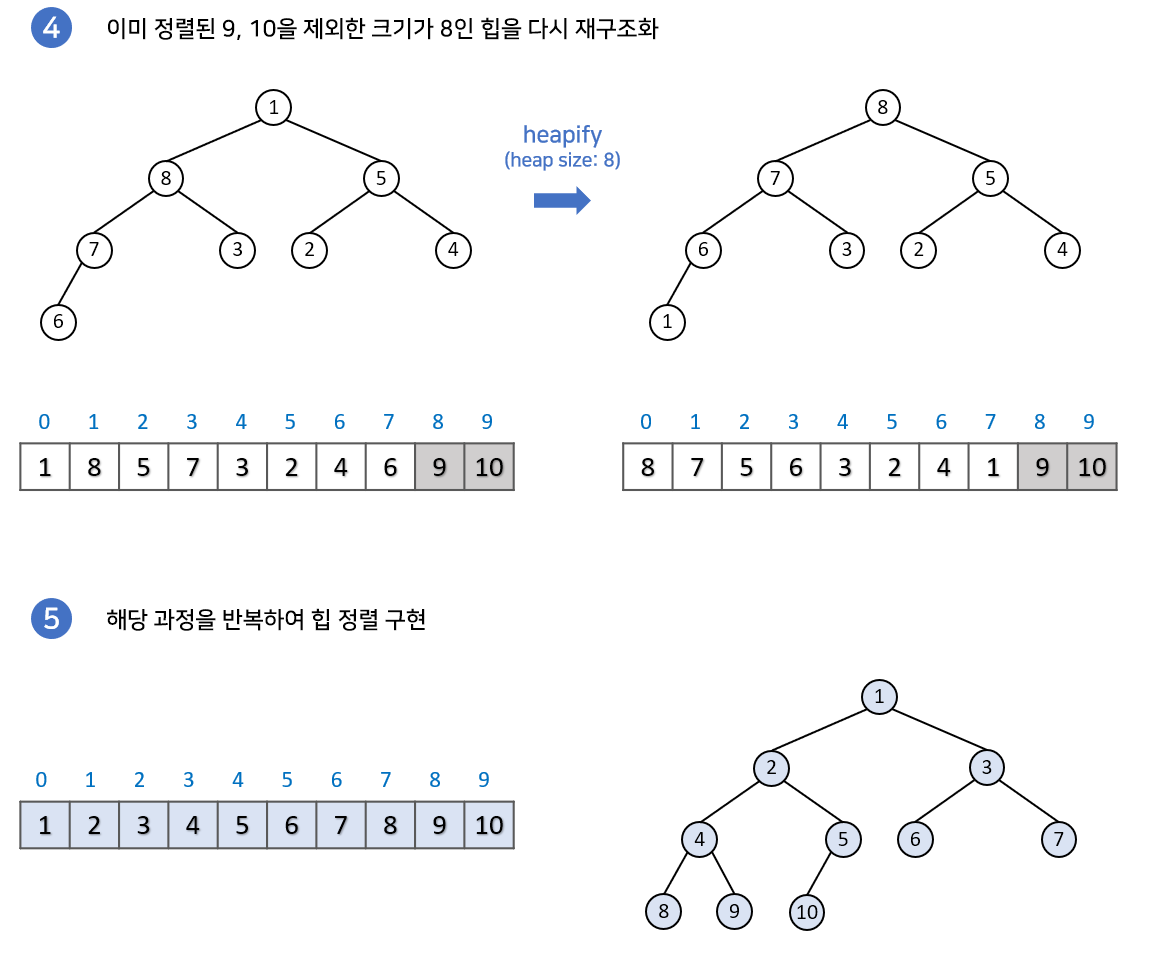
4) 추출 및 재구성 과정 반복:
2번과 3번 단계를 반복하여 최대값을 추출하고 힙을 재구성함. 이 과정을 모든 요소가 추출될 때까지 반복함.
힙 정렬은 안정적인 정렬 알고리즘으로 알려져 있으며, 평균 및 최악의 경우에도 시간 복잡도가 O(n log n)임.
힙 정렬은 추가적인 메모리 공간을 필요로 하지 않는 인-장(in-place) 정렬 알고리즘으로 분류됨.
대규모 데이터를 정렬하는 데 효과적이며, 힙 자료구조를 구성하는 과정이 추가적인 시간을 요구하지만
추출 및 재구성 과정에서는 빠른 속도를 제공함.
따라서 힙 정렬은 우선순위 큐와 같이 최대값/최소값을 빠르게 찾아야 하는 상황에 유용하게 사용될 수 있음.
heap_sort(): build_heap() for i <- n-1 down to 1 list[i] <-> delete_max() # list[0] 바꿔주면서 관심범위 조정 |
12-3-1. 구현
from my_heap import Heap
def heap_sort(alist):
blist = [element for element in alist]
h = Heap(blist)
for i in range(len(blist)-1, 0, -1):
alist[i] = h.delete_max()
# 관심 범위를 조정한 heap_sort
def heap_sort_ipv(alist):
build_heap(alist)
for last in range(len(alist)-1, 0, -1):
alist[last], alist[0] = alist[0], alist[last]
percolate_down(alist, 0, last-1)
def build_heap(alist):
for i in range((len(alist)-2)//2, -1, -1):
percolate_down(alist, i, len(alist)-1)
# end : 관심 범위 축소 지정
def percolate_down(alist, parent: int, end: int):
child = 2*parent + 1
right = 2*parent + 2
if child <= end:
if right <= end and alist[child] < alist[right]:
child = right
if alist[parent] < alist[child]:
alist[parent], alist[child] = alist[child], alist[parent]
percolate_down(alist, child, end)
# import random as r
# list_ex = [r.randint(1,20) for _ in range(20)]
# print(list_ex)
# heap_sort(list_ex)
# print(list_ex)
12-3-2. 테스트
import random as r
list_ex = [r.randint(1,30) for _ in range(20)]
print(list_ex)
heap_sort_ipv(list_ex)
print(list_ex)
12-3-3. 내장 라이브러리 사용
import heapq
import random as r
def heap_sort_lib(alist):
h = [ ]
for element in alist:
heapq.heappush(h, element)
return [heapq.heappop(h) for i in range(len(h))]
liex = [r.randint(1,30) for _ in range(20)]
print(liex)
result = heap_sort_lib(liex)
print(result)




