Optimization_여행하는 외판원 문제: 문제 기반

참고 문서: https://kr.mathworks.com/help/optim/ug/traveling-salesman-problem-based.html

여행하는 외판원 문제: 문제 기반 - MATLAB & Simulink - MathWorks 한국

 

목적: 여러 경유지(도시)를 거쳐 원래 도시로 다시 돌아오는 최단 순회 경로를 구하는 것

 

위의 예제에는 200개의 경유지를 선택했지만, 사용자는 nStops 변수를 변경하여 손쉽게 문제의 규모를 정할 수 있습니다.

 

초기 문제를 풀면 해에 하위 경로가 있음을 확인할 수 있습니다. 즉, 문제에서 구한 최적해가 모든 점을 통과하는 하나의

연속적인 경로를 제공하는 것이 아니라, 연속되지 않은 여러 개의 루프를 가지고 있음을 의미합니다.

 

그런 다음, 하위 경로를 확인하고 제약 조건을 추가한 후 하위 경로가 제거될 때까지 최적화를 다시 실행하는 반복적인

작업을 하게 될 것입니다.

 

 

 

1. 문제 정식화

 

다음과 같이 정수 선형 계획법을 사용하는 여행하는 외판원 문제를 정식화합니다.

• 가능한 모든 여행(trip), 즉 서로 다른 모든 경유지 쌍을 생성합니다.
• 각 여행의 거리를 계산합니다.
• 최소화할 비용 함수는 경로에 포함된 각 여행 거리의 합입니다.
• 결정 변수는 이진 변수이고 각 여행과 연결되어 있습니다. 여기서 1은 경로에 존재하는 여행을 나타내고, 0은 경로에 존재하지 않는 여행을 나타냅니다.
• 경로에 모든 경유지가 포함되도록 하기 위해 각 경유지가 정확히 두 개의 여행에 존재하도록 규정하는 선형 제약 조건을 포함시켜야 합니다. 이는 각 경유지에서 도착과 출발이 각각 한 번씩 일어남을 의미합니다.

 

2. 경유지 생성하기

 

대략적으로 미 대륙을 나타내는 다각형 내부에 임의 경유지를 생성합니다.

 

→ 미국의 국경 데이터를 사용하여 10개의 무작위 정지점 좌표를 생성하고, 이러한 좌표가 미국 국경 내에 있는 경우 저장

 

 

load('usborder.mat', 'x', 'y', 'xx', 'yy'); % usborder.mat에서 x, y, xx, yy 변수를 로드해옴 rng(3, 'twister') % rng(): 난수발생기의 초기 시드값 설정 nStops = 10; % 정지점의 수 = 임의로 설정 가능 ★  예제에서는 200개로 설정했으나, 여기서는 10개로 축소. stopsLon = zeros(nStops, 1) % stopsLon과 stopsLat를 (10,1)의 zero로 메모리 사전할당 stopsLat = stopsLon; n = 1; while (n <= nStops) % n이 10보다 작거나 같을 때 까지 실행함     xp = rand*1.5; % xp변수에 0~1.5 사이의 무작위 수를 할당 // 경도의 예상좌표     yp = rand; % yp변수에 0에서 1사이의 무작위 수를 할당 // 위도의 예상좌표     if inpolygon(xp, yp, x, y) % inpolygon() 함수 사용: xp 및 yp 좌표가 x, y로 주어진 다각형 내에 있는지 확인         stopsLon(n) = xp; % 만약 좌표가 미국 국경 내에 있다면, 해당 좌표를 stopsLon과 stopsLat 변수에 저장함         stopsLat(n) = yp;         n = n+1; % 정지점 수를 증가     end end

 

 

3. 점 간의 거리 계산하기

 

10개의 경유지가 있으므로 여행 횟수는 45개입니다. 즉, 이진 변수가 45개임을 의미합니다

 

(변수 개수 = 10개 중에서 2개를 선택하는 경우의 수).

 

모든 여행, 즉 모든 경유지 쌍을 생성합니다.

 

피타고라스 규칙을 사용할 수 있도록 지구가 평평하다고 간주하고 모든 여행 거리를 계산합니다.

 

idxs = nchoosek(1:nStops,2);  % nchoosek(): nCk combination // 10개의 정지점에서 뽑을 수 있는 모든 경로의 수 // 10C2는 45이다.  dist = hypot(stopsLat(idxs(:,1)) - stopsLat(idxs(:,2)), ...              stopsLon(idxs(:,1)) - stopsLon(idxs(:,2)));  % hypot(a, b): a제곱과 b제곱의 합의 제곱근 // 45개 경로에 대한 45가지의 길이 lendist = length(dist); % dist의 갯수

 

위와 같이 dist 벡터에 대한 정의를 사용하면 경로 길이는 다음과 같습니다.

 

dist'*trips

 

여기서 trips는 해에서 구한 여행 횟수를 나타내는 이진 벡터입니다.

 

이 경로의 길이가 바로 최소화하고자 하는 경로의 거리입니다.

 

 

4. 그래프 생성 및 지도 그리기

 

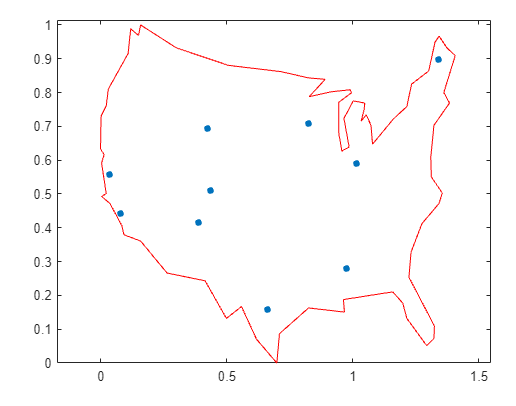
문제를 그래프로 나타냅니다. 경유지를 노드로 나타내고 여행을 간선으로 나타내는 그래프를 생성합니다.

 

→ G 그래프를 시각화하고, 그래프의 정점은 stopsLon과 stopsLat 배열로 표시되며, 그래프에는 미국의 국경이 나타남.

 

G = graph(idxs(:,1),idxs(:,2));

 

그래프 플롯을 사용하여 경유지를 표시합니다. 그래프 간선 없이 노드를 플로팅합니다.

 

 

figure hGraph = plot(G, 'XData', stopsLon, 'YData', stopsLat, 'LineStyle', 'none', 'NodeLabel', {});  % Linestyle: none으로 설정하여 엣지를 선으로 그리지 않음 % NodeLabel: {} 정점에 레이블을 표시하지 않음 hold on plot(x, y, 'r-') hold off

 

 

 

5. 변수와 문제 생성하기

 

잠재적 여행을 나타내는 이진 최적화 변수를 갖는 최적화 문제를 생성합니다.

 

 

tsp = optimproblem; % tsp라는 최적화 문제 객체를 생성 trips = optimvar('trips', lendist, 1, 'Type', 'integer', 'LowerBound', 0, 'UpperBound', 1); % optimvar(): 최적화 변수를 생성하는 함수 % 최적화 변수의 크기: 1 → 각 최적화 변수는 1차원 벡터로 정의된다는 의미 % 최적화 변수의 유형: integer(정수) % 최적화 변수의 하한값: 0 % 최적화 변수의 상한값: 1

 

문제에 목적함수를 포함시킵니다.

 

tsp.Objective = dist'*trips; % 최적화 문제 객체인 tsp에 목적함수인 Objective를 포함

 

 

6. 제약 조건

 

각 경유지마다 도착하는 여행과 출발하는 여행이 각각 하나씩 있어야 하므로,

 

경유지마다 두 개의 여행이 연결되어 있는 선형 제약 조건을 생성합니다.

 

그래프 표현을 사용해 경유지에 연결된 모든 간선을 찾아 해당 경유지에서 시작하거나 끝나는 모든 여행을 식별합니다.

 

→ 경유지마다 해당 경유지에 대한 여행의 합을 2로 규정하는 제약 조건을 생성합니다.

 

constr2trips = optimconstr(nStops, 1); % optimconstr(): 빈 최적화 제약조건 배열 생성 for stop = 1:nStops     whichIdxs = outedges(G, stop);      % outedges(): 현재 정지점으로부터 진출할 수 있는 정지점들 (1번 정지점 => 9개의 점으로 진출할 수 있음)     constr2trips(stop) = sum(trips(whichIdxs)) == 2; % 각 정지점에서 2번의 이동만 가능함 (제약조건) end tsp.Constraints.constr2trips = constr2trips;  % 최적화 문제 객체인 tsp에 제약조건인 Constraints를 포함  → 각 정지점에서의 이동횟수에 대한 제약조건이 최적화문제에 적용됨

 

 

7. 초기 문제 풀기

 

이제, 문제를 풀 준비가 되었습니다. 반복 출력값을 표시하지 않으려면 디폴트 표시를 끄십시오.

 

opts = optimoptions('intlinprog', 'Display','off');  % optimoptions 함수를 사용하여 정수 선형 프로그래밍 최적화 알고리즘을 위한 옵션 설정을 생성 % intlinprog: 최적화 알고리즘으로 사용될 정수 선형 프로그래밍 알고리즘을 지정함 % Display off : 최적화 알고리즘 실행 중의 출력 메시지 표시 x tspsol = solve(tsp, 'Options',opts) % solve 함수를 사용하여 최적화 문제(tsp)를 해결하고 최적 해(solution)를 찾음

 

 

8. 해 시각화하기

 

해에서 구한 여행을 간선으로 사용하여 새 그래프를 생성합니다.

 

이를 위해, 값이 정확히 정수가 아닌 경우에는 해를 반올림한 후 결과 값을 logical형으로 변환합니다.

 

→ 최적 해(tspsol)를 처리하고 최적 경로에 대한 그래프(Gsol)를 생성하는 작업

 

 

tspsol.trips = logical(round(tspsol.trips)); % 각 경로가 선택되었는지의 여부를 나타내는 이진변수로의 변환 Gsol = graph(idxs(tspsol.trips, 1), idxs(tspsol.trips, 2), [], numnodes(G)); % 최적 경로를 나타내는 이진 변수(tspsol.trips)를 기반으로 최적 경로를 나타내는 그래프 생성

 

기존 플롯에 새 그래프를 중첩하고 간선을 강조표시합니다.

 

 

hold on highlight(hGraph, Gsol, 'LineStyle','-') % highlight(): 간선을 강조표시 title('Solution with Subtours')

 

지도에서 알 수 있듯이 해에는 여러 하위 경로가 있습니다.

 

지금까지 지정한 제약 조건은 이러한 하위 경로의 발생을 막지 않습니다.

 

어떤 하위 경로의 발생도 허용하지 않으려면 엄청나게 많은 수의 부등식 제약 조건이 필요할 것입니다.

 

 

 

 

9. 하위 경로 제약 조건

 

모든 하위 경로 제약 조건을 추가할 수는 없으므로 반복법을 사용하십시오.

 

현재 해에서 하위 경로를 검출한 후 부등식 제약 조건을 추가하여 특정 하위 경로가 발생하지 않도록 합니다.

 

이렇게 하면 몇 번의 반복으로 적합한 경로를 찾을 수 있습니다.

 

부등식 제약 조건을 사용하여 하위 경로를 제거합니다.

 

예를 들어, 하위 경로에 5개의 점이 있다고 하면 이 점을 연결하는 5개의 직선이 하위 경로를 생성하게 됩니다.

 

이 5개의 점 사이의 직선의 개수가 4개보다 작거나 같아야 함을 나타내는 부등식 제약 조건을 만들어 이 하위 경로를

제거하십시오.

 

이 5개 점 사이의 모든 직선을 찾은 후 존재하는 직선의 개수가 4개를 넘지 않도록 해에 제약 조건을 적용합니다.

 

해에 5개 이상의 직선이 존재하면 해에 하위 경로가 생기기 때문에 이는 올바른 제약 조건입니다

(n개 노드와 n개 간선이 포함된 그래프는 항상 순환을 포함함).

 

현재 해에서 간선을 사용하여 생성한 그래프인 Gsol의 연결성분을 식별하여 하위 경로를 검출합니다. 

 

conncomp는 각 간선이 속한 하위 경로 개수를 가진 벡터를 반환합니다.

 

→ 최적 경로 그래프인 Gsol에서 서브투어(subtour)의 수를 식별하고 출력

 

tourIdxs = conncomp(Gsol); numtours = max(tourIdxs); % 서브투어(경로 묶음)의 수를 결정  fprintf(' # of subtours: %d\n', numtours);

 

 

 

선형 부등식 제약 조건을 포함시켜 하위 경로를 제거하고 단 하나의 하위 경로만 남을 때까지 솔버를 반복해서 호출합니다.

 

→ TSP의 최적 경로를 찾고, 서브투어 제약 조건을 만족하도록 최적화 알고리즘을 반복적으로 실행하여

 

최적 해를 찾습니다. 결과적으로 최적 해는 서브투어가 없는 최적 경로를 나타내며, 이를 그래프로 시각화합니다.

 

k = 1; while numtours > 1 % numtours가 1 이상인 경우 계속 반복 → 1 미만일 때 까지 계속 순회     for ii = 1:numtours         inSubTour = (tourIdxs == ii);         a = all(inSubTour(idxs), 2);         constrname = "subtourconstr" + num2str(k);         tsp.Constraints.(constrname) = sum(trips(a)) <= (nnz(inSubTour) - 1);         k = k+1;     end     [tspsol, fval, exitflag, output] = solve(tsp, 'options',opts);     tspsol.trips = logical(round(tspsol.trips));     Gsol = graph(idxs(tspsol.trips,1),idxs(tspsol.trips,2),[],numnodes(G));      % 최적 해를 기반으로 최적 경로를 나타내는 그래프 Gsol을 생성     hGraph.LineStyle = 'none'; % 그래프 시각화에서 선 스타일을 제거     highlight(hGraph, Gsol, 'LineStyle', '-')     drawnow     tourIdxs = conncomp(Gsol);     numtours = max(tourIdxs);     fprintf('# of subtours : %d\n', numtours) end title('Soultion with Subtours Eliminated'); hold off

 

 

 

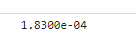
10. 해의 품질

 

해는 하나의 폐루프(閉 Loop)이므로 하나의 실현 가능한 경로를 나타냅니다.

 

하지만 이것이 최소 비용 경로일까요? 이를 확인하는 한 가지 방법은 출력 구조체를 검사하는 것입니다.

 

절대 간격이 작다는 사실은 해가 최적이거나 해의 총 길이가 최적에 가깝다는 것을 의미합니다.

 

disp(output.absolutegap)